工具機空間精度補償實務與效果
空間精度體積誤差補償技術,被視為提升加工品質的核心解決方案。此技術通過系統化分析與修正工具機在三維工作空間內的綜合誤差,顯著降低因機械結構缺陷、環境干擾或加工負載所導致的精度偏差,從而實現高階工件(如航太零件、醫療器械、光學模具)的嚴格公差要求。實務上,空間精度補償技術能將工具機的體積誤差減少50%至90%。本案以TYPE B五軸機進行研究,採用Etalon雷射追蹤儀進行量測,搭配海德漢TNC 640控制器其空間精度52號選配功能進行補償;以本案五軸加工中心為例,未補償前空間誤差達20微米,經補償後可穩定控制於10微米以內,本文將詳細說明其研究測試過程與結果。
工具機幾何21項誤差
工具機的誤差可分為單軸幾何誤差、軸間垂直度誤差,其兩者合計21項,是影響精度的主要因素。三軸幾何誤差(18項),其每個線性運動軸(X/Y/Z軸)在移動時,會產生6項自由度誤差(3平移+3旋轉),三軸共18項。圖1單軸為例:
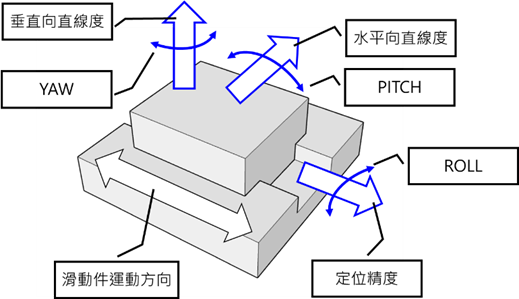 |
三軸21項自由度誤差說明如下:
(1)線性定位誤差(Linear Positioning Error)
(2)水平直線度誤差(Horizontal Straightness Error)
(3)垂直直線度誤差(Vertical Straightness Error)
(4)俯仰誤差(Pitch Error)
(5)偏擺誤差(Yaw Error)
(6)滾動誤差(Roll Error)
(7)垂直度誤差(Squareness Error)
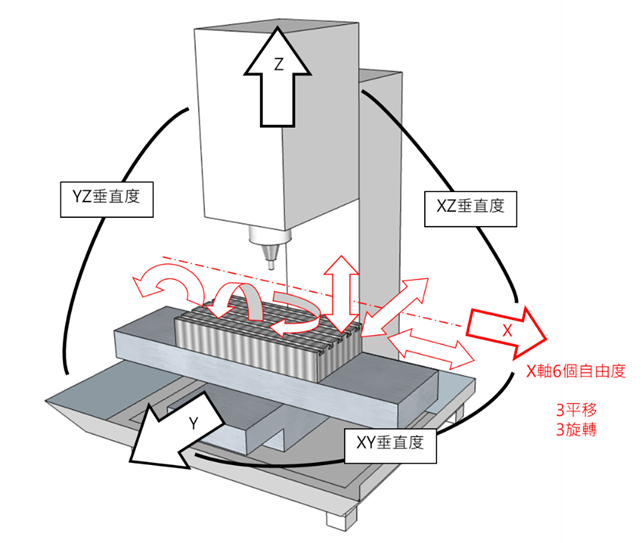
圖2說明三軸21項自由度誤差:
 |
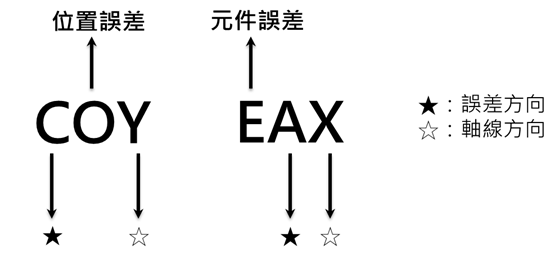
國際標準ISO230-1將幾何誤差項目名稱定義為元件誤差(6自由度)及位置誤差(垂直度)。為方便理解,圖3做兩個誤差名稱定義說明:
(1) COY:Y軸在C方向的位置誤差;此即代表X軸與Y軸間的垂直度。
(2) EAX:X軸在A方向的誤置誤差;此即代表X軸的俯仰誤差(Pitch Error)。
 |
依據ISO230-1標準,工具機21項自由度誤差定義如下圖所示:
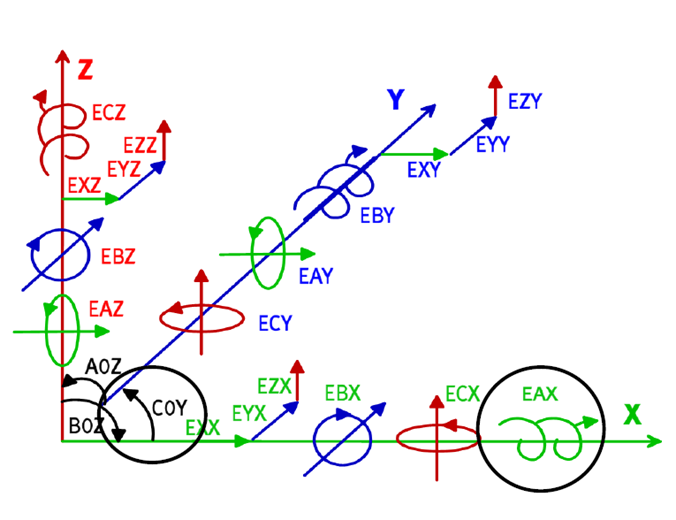 |
Source: ISO 203-1
空間精度說明
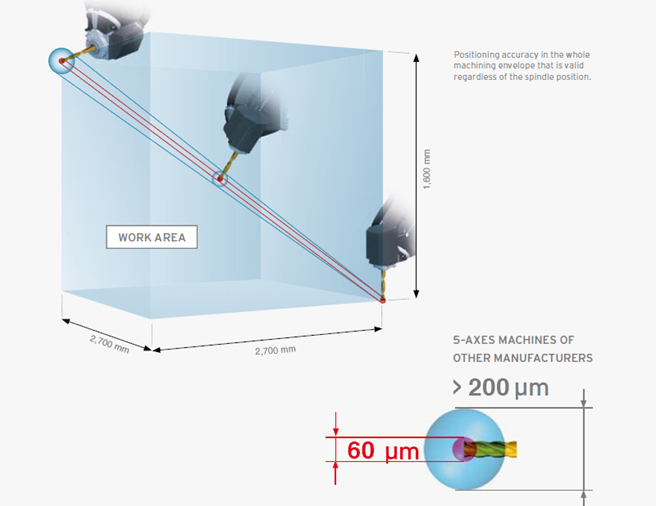
目前空間精度誤差係指體積精度誤差,其為幾何精度綜合表現,其定義為工具機體積內任何位置的目標與實際位置之間的最差情況,為X方向、Y方向、及Z方向之最大誤差之向量長度。
為方便理解,舉例 DMG Mori 工具機:其網站宣稱其2.7米行程之工具機,其體積誤差透過精密鏟花製程可控制60um以下。
 |
Etalon雷射追蹤儀量測空間精度與規劃
目前雷射追蹤儀(ETALON LASERTRACER-NG)為工具機量測體積誤差高精度的量測設備,其構造參考下圖:
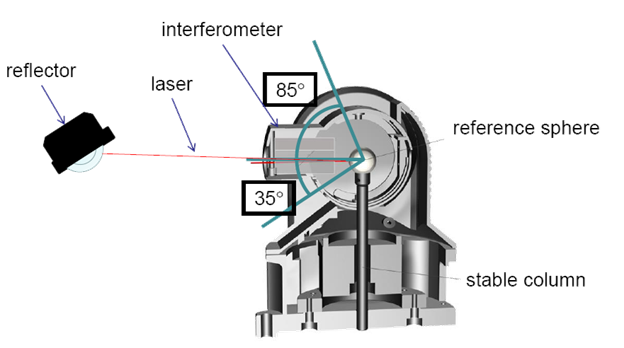 |
Source: Etalon (2025)
雷射追蹤儀其量測長度可達20m,且由於本體具有相當的體積與重量(230mm;8.5kg),故較適合中、大型工具機量測。其解析度可到0.001um,故除了適合量測與補償工具機,其相關技術亦也用在CMM領域。圖7為規格表:
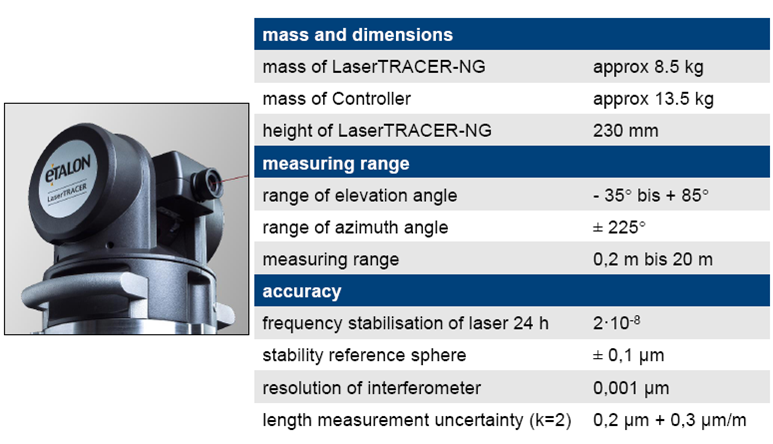 |
 |
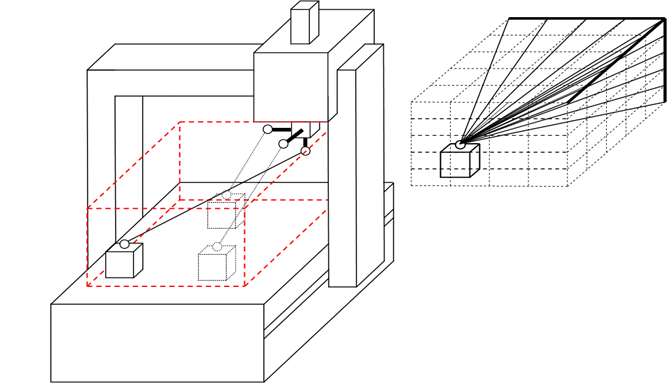
追蹤儀量測原理:將GPS量測原理運用在工具機,僅能量測出長度數據(1D Laser)。
(1) 透過相對長度進行位置計算,非直接量測出角度誤差。
(2) 空間量測需要在4個角落位置測量(至少三位置)。
(3) 干涉儀多邊量測法(Multilateration method)。
 |
雷射追蹤儀進行空間精度量測補償規劃
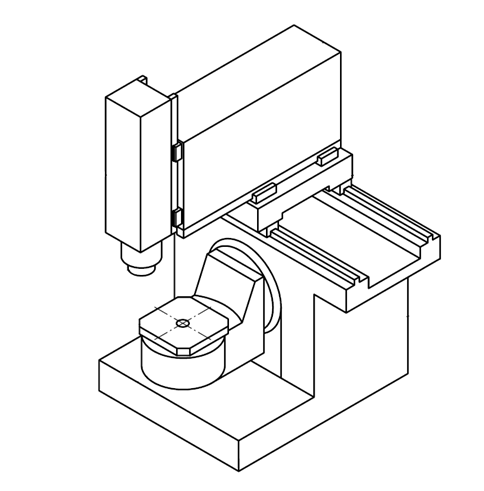
本案目的為了解空間精度補償效果,故選定一台具有空間補償功能之五軸機:
機台:B TYPE
控制器:海德漢TNC 640控制器
量測行程:620mmx520mmx460mm
 |
量測規劃流程如下:
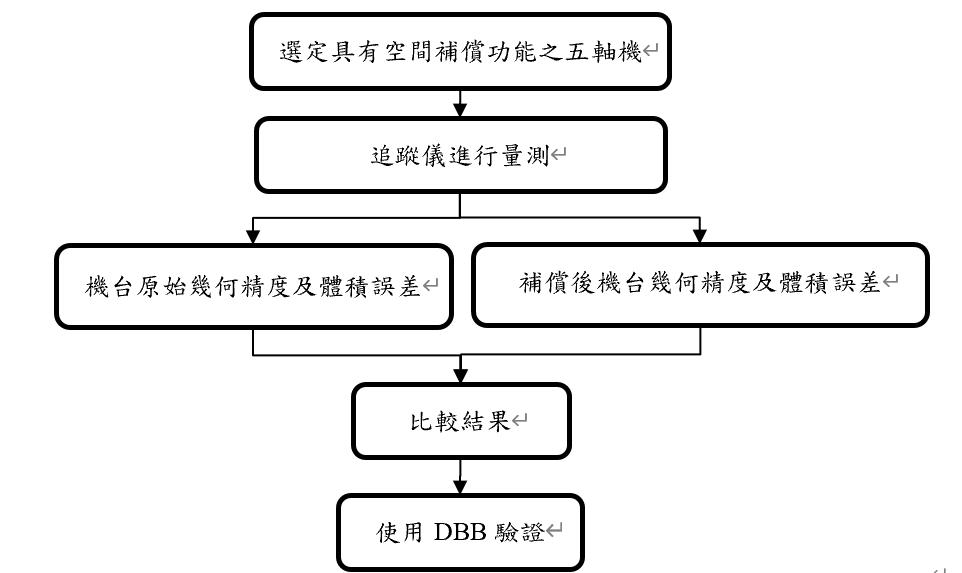 |
使用追蹤儀進行量測與補償:量測注意事項與觀念說明如下。
需設置4個或更多的量測位置(21個自由度至少6-7個位置):
(1) 通常是在角落位置,且不同的高度設置。
(2) 追蹤儀架設於治具平台並確認是否穩固。
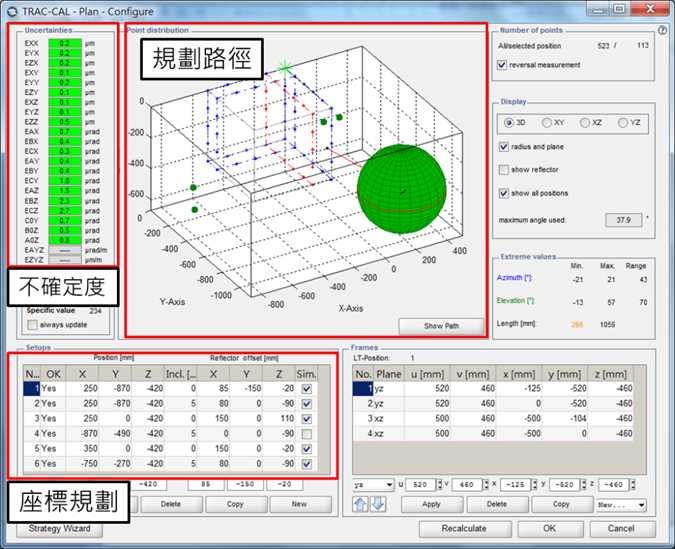
(3) 規劃路徑時,以空間體方盒子(BOX)設定,第一種方式是將追蹤儀設置於量測空間外,另一種方式是追蹤儀於量測空間內,固需移除干涉平面,以利量測進行。
(4) 其4個位置可不需變換貓眼的偏置(offset)。而最後2-3個位置需變換貓眼的偏置(offset),但量測平面可以省略為2平面量測,且2平面間距離差距最大越好。
 |
 |
空間精度量測結果:原始與補償後精度分析
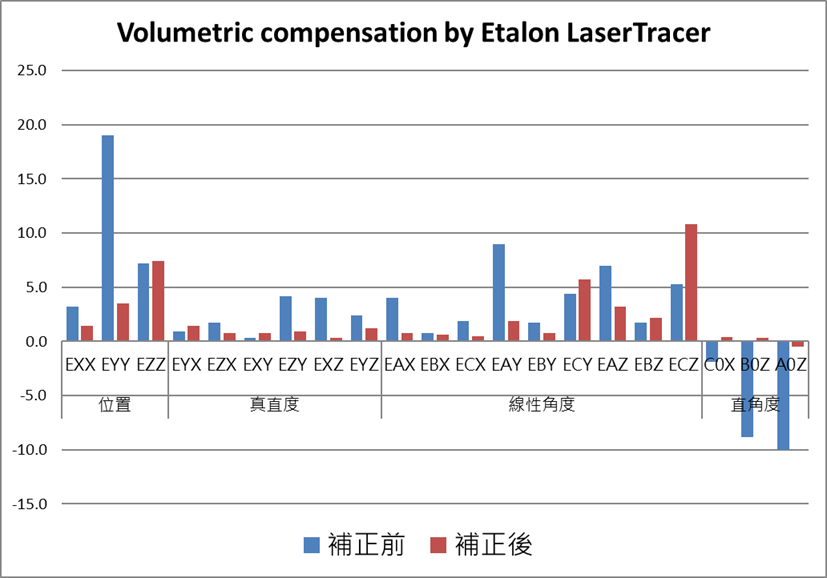
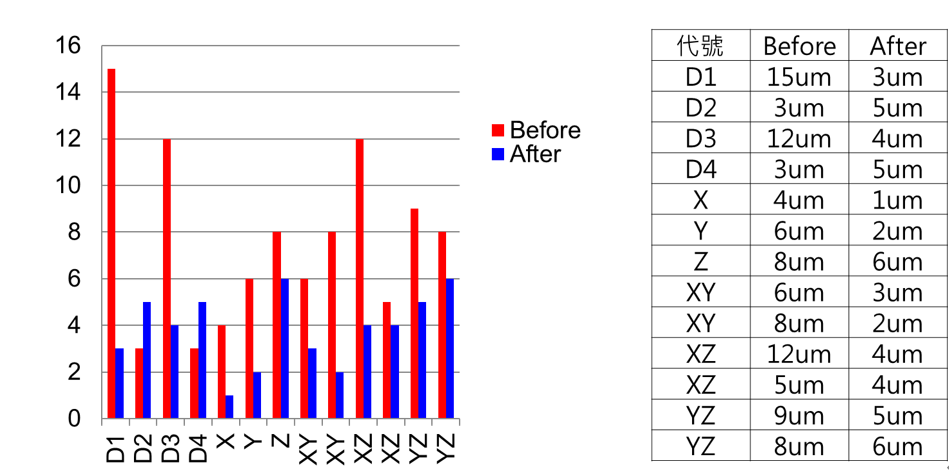
量測完比較原始及補償後21項幾何誤差數據,可得知經補償後誤差大幅降低,透過統計分析可得知其改善精度達76%,以下圖表為實測數據。
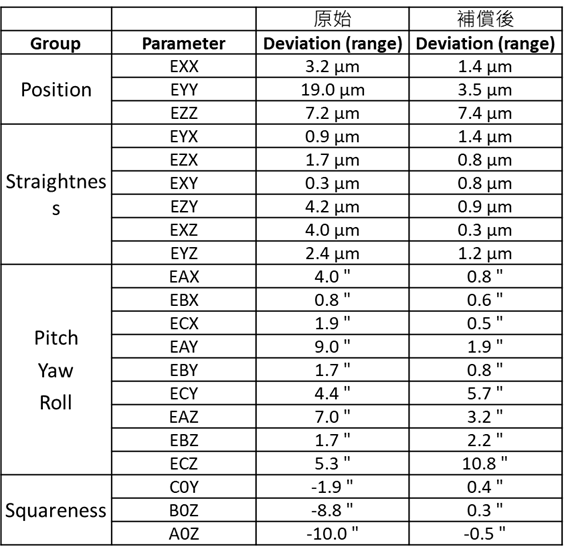 |
當前精密製造與高階量測領域對空間精度的要求日益嚴苛,如何有效提升系統的整體精度成為關鍵課題。透過對空間21項自由度誤差進行全面補償,本次研究顯著提升了精度表現,整體空間精度改善幅度高達76%,成果令人矚目。
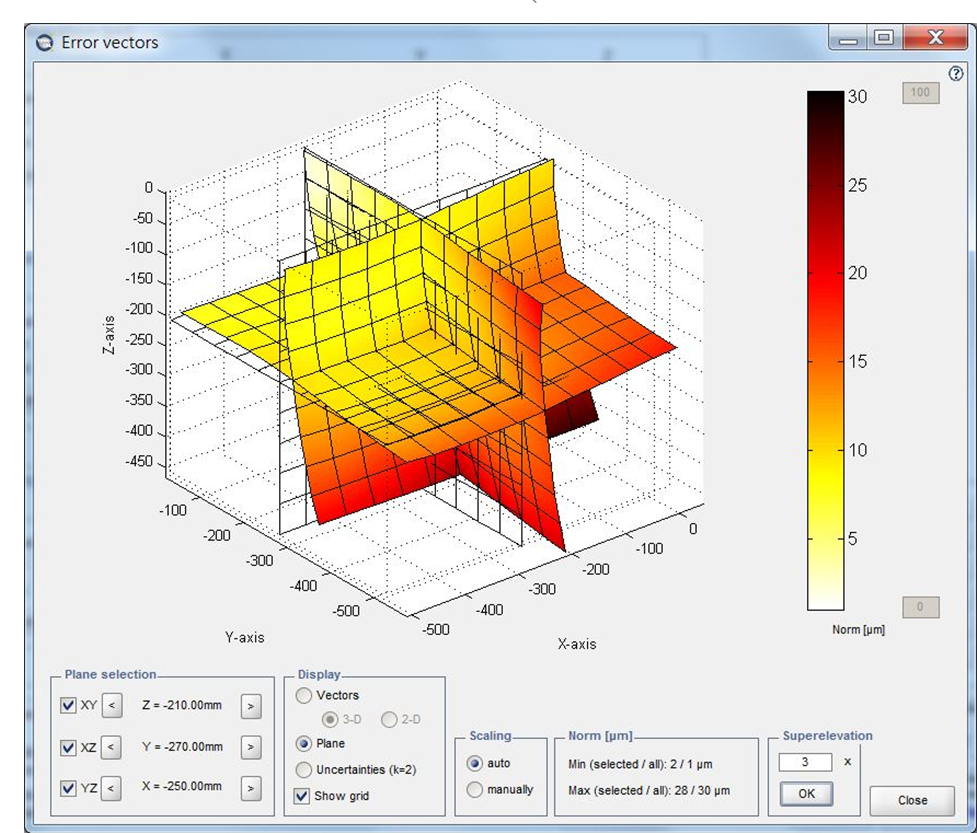
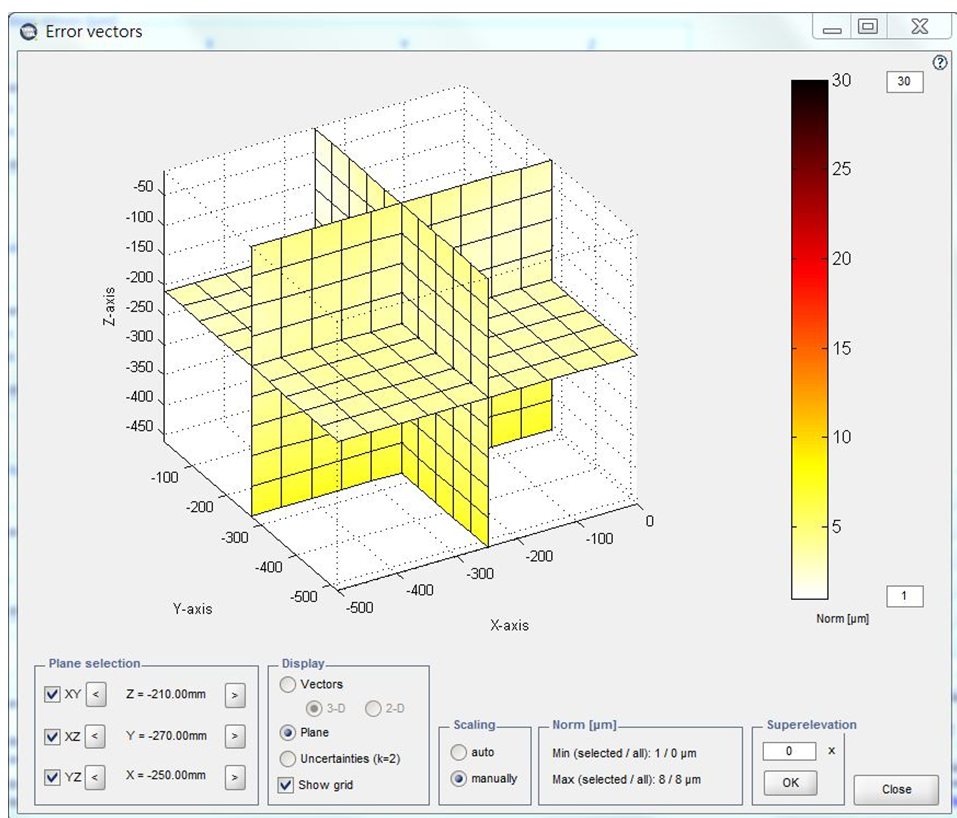
所謂空間21項自由度誤差,涵蓋了三維空間中位置與姿態的各種偏差,包括三軸線性誤差、角度誤差與交互耦合誤差等,這些微小偏差往往會在精密加工或測量中累積並放大,對最終結果造成重大影響。因此,本研究透過建構完整的誤差模型,搭配高精度感測器與演算法分析,逐一識別並補償各項誤差來源,有效提升整體定位與量測準確度。更值得一提的是,體積誤差方面亦獲得大幅改善,原始系統的體積誤差約為30um,經補償後下降至僅9um。不僅展現出誤差補償技術的實質效益,也對未來高精度應用提供了具體可行的技術路徑,無論是在工具機校正、精密量測平台或自動化檢測系統中皆具備高度應用潛力。
 |
 |
 |
空間精度量測結果:軟體模擬補償前後對角線數據
為驗證空間誤差補償的實際成效,本研究進一步透過空間對角線模擬,進行補償前後的精度比較分析。空間對角線模擬是評估整體空間精度的有效方法,因其涵蓋了設備三維運動的複雜路徑,特別能揭示系統在跨區域運動時所產生的綜合性誤差。在本次實驗中,雷射追蹤儀被用來量測設備在空間對角線方向上的實際位置變化,並與理論座標進行比對,以評估補償效果。
為驗證空間誤差補償的實際成效,本研究進一步設計並實施空間對角線模擬測試,進行補償前後的精度比較分析,結果顯示補償後成效顯著。空間對角線模擬是一種評估三維設備整體空間精度的有效方法,因其涵蓋了機台在三個軸向同時運動時所形成的複雜路徑。與僅針對單一軸向進行測試相比,空間對角線模擬能更全面地反映系統在實際應用中可能遭遇的綜合性誤差,特別是跨越多個運動區域時所引發的位置偏差。本次實驗中,研究團隊使用高精度雷射追蹤儀對設備於空間對角線運動過程中的實際位置進行量測,並與預定之理論座標進行比較分析。雷射追蹤儀具備高解析度與高重複性,能即時擷取運動軌跡中的微小偏移,為誤差分析提供精確的量測依據。透過收集補償前與補償後的座標數據,能清楚辨識出誤差補償系統對空間運動精度的改善效果。
透過雷射追蹤儀模擬出對角線量測結果,床身對角→4條;床面對角→6條;中間位置→3條。共有13條對角線數據,示圖如圖18。
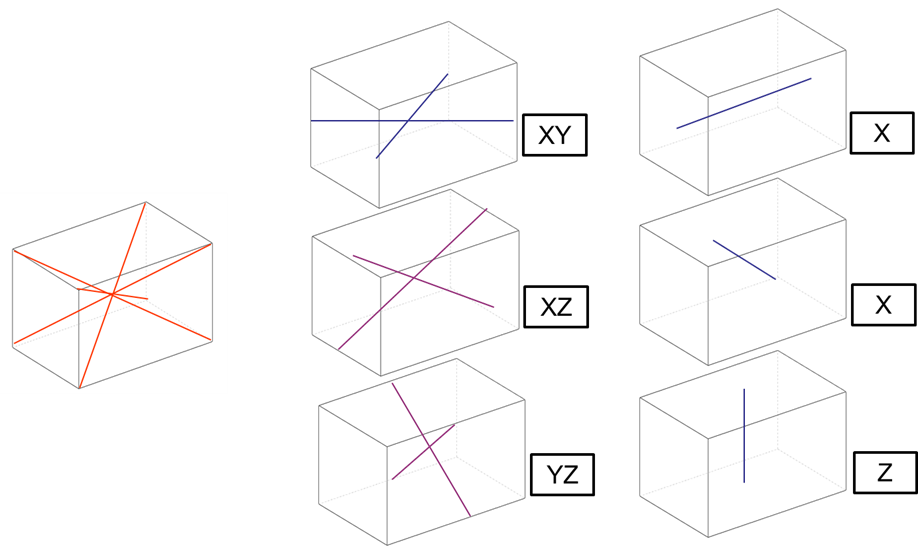 |
補償前的量測結果顯示,對角線方向的最大誤差仍存在明顯偏差,對整體精度造成潛在影響。然而,經由本研究所建立之21項自由度誤差補償後,再進行相同對角線路徑的模擬量測,結果顯示其精度改善幅度達到50%,誤差幅度明顯降低,顯示補償後對實際三維運動誤差具有良好修正能力。
 |
空間精度量測結果:實作對角線驗證
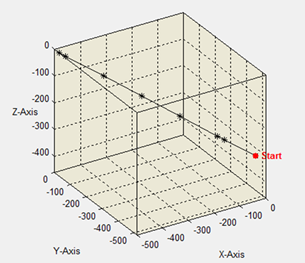
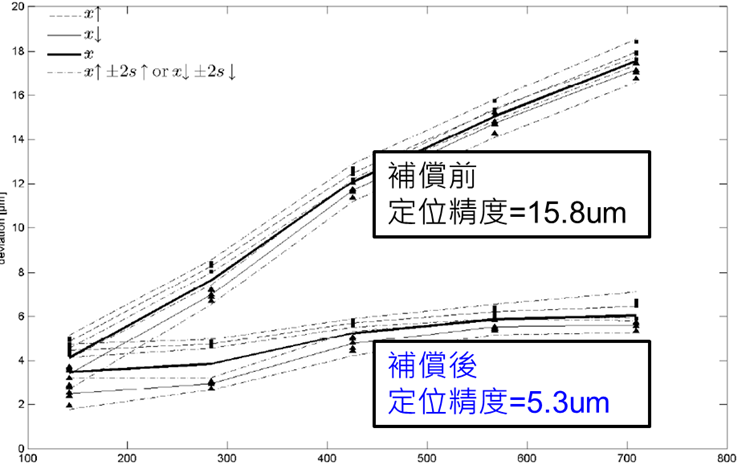
在現代高精度製造與量測技術中,如何有效掌握並改善設備於空間運動過程中的定位誤差,是提升整體系統精度的關鍵所在。本研究特別針對ISO 230-6標準中所定義的體積內對角線量測項目進行實測,藉由雷射追蹤儀對機台進行對角線D1之量測,進一步驗證誤差補償技術的實際成效。依據ISO 230-6規範,對角線量測是評估機器設備在三維空間內整體幾何精度的有效方法,特別能反映出機構在多軸聯動下的綜合誤差狀況。本次選定的體積對角線D1跨越整個工作空間,為系統運動精度的關鍵代表指標。量測過程中,透過高精度雷射追蹤儀進行實際座標比對,補償前D1的定位誤差為15.8um,經由誤差補償模型修正後,誤差成功減低至5.3um,精度提升超過三倍,改善幅度顯著。
更具代表性的是,此次量測結果與先前透過軟體模擬所推估的補償效益高度吻合,顯示誤差模型在實務應用中具備良好的預測準確度與一致性。此一驗證不僅提升了對補償模型的信任度,也證實了模擬系統可作為未來設備校正與設計優化的重要工具,進一步降低實驗成本與時間。
Figure 20 以雷射追蹤儀進行對角線D1量測

 |
總結而言,透過ISO 230-6實際對角線量測案例,有效展示了誤差補償技術對於空間精度的實質改善。結合雷射追蹤儀的高精度特性與模擬模型的預測能力,不僅提升量測效率與精度,也為機械設備未來導入智慧補償控制提供明確方向。此成果對於精密加工、自動化檢測及高階機台開發皆具高度應用價值。
空間精度量測結果:實作DBB循圓驗證
在高精密工具機的性能驗證中,循圓量測儀(Ballbar)被廣泛用作評估系統幾何精度的重要工具。其透過兩軸圓形插補運動所形成的圓軌跡,能有效反映機台在實際運動中所產生的誤差情形,特別是對真圓度、直線度與垂直度等幾何精度參數具有高度靈敏度。本研究即以循圓量測儀進行工具機三大主平面(XY、YZ、XZ)之全圓測試,全面檢視誤差補償技術在動態運動精度上的實質改善效果。
 |
首先,在XY平面的測試中,未補償前的真圓度誤差為3.7μm,經誤差補償後,顯著降低至2.6um,改善幅度約30%。此平面代表機台最常使用之工作平面,因此其精度提升對加工品質有直接正向影響。
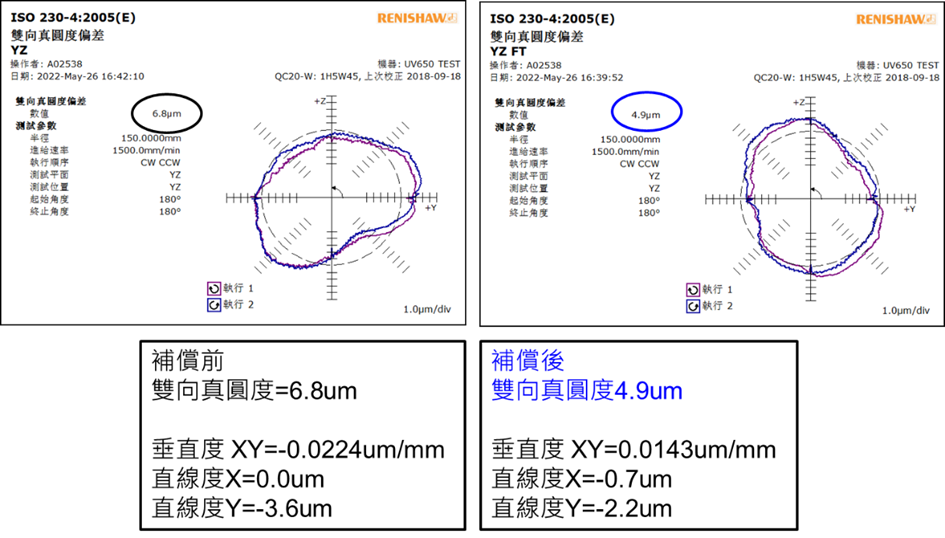
在YZ垂直平面的量測中,補償前的真圓度誤差為6.8um,補償後下降至4.9um,顯示誤差補償技術同樣在垂直軸聯動上具有良好的效果。此外,由於YZ平面常被用於深孔加工與側向刀具運動,其精度改善對於確保零件垂直特徵之幾何準確性具有關鍵意義。
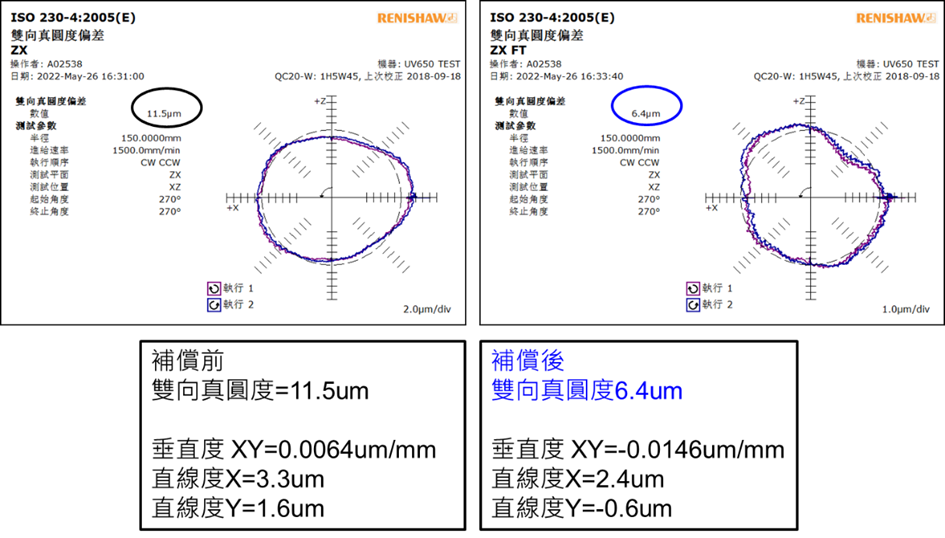
至於XZ平面,補償前的真圓度誤差為11.5um,為三個平面中最大,顯示原始在此方向的幾何偏差較為嚴重。然而經過補償後誤差顯著下降至6.4um,改善幅度超過44%,顯示補償模型在不同方向皆具一致性的修正能力。
除了真圓度之外,本次循圓量測亦同步比較了三平面間的垂直度與直線度誤差。經補償後,平面間的正交性趨於穩定,且軸向運動的直線度變化也呈現收斂現象。這意味著誤差補償不僅能改善單一量測參數,更有助於提升整體機台幾何結構的協調性與穩定性。整體而言,透過三平面循圓量測所獲得的實測數據,充分驗證誤差補償技術在提升機台動態運動精度方面的實質效益。
 |
 |
 |
總結與未來展望
以下總結本文章重點:
1. 三軸工具機具有21項自由度誤差(三軸幾何誤差18項,三平面垂直度3項)。
2. 空間精度誤差係指體積精度誤差,其為幾何精度綜合表現,其定義為工具機體積內任何位置的目標與實際位置之間的最差情況,為X方向、Y方向、及Z方向之最大誤差之向量長度。
3. 補償後21項幾何誤差數據,誤差大幅降低其改善精度達76%
4. 原始的體積誤差約為30um,經補償後下降至僅9um。
5. 對角線路徑的模擬量測,結果顯示其精度改善幅度達到50%。
6. 實作對角線誤差,補償前D1的定位誤差為15.8μm,經由誤差補償模型修正後,誤差成功降低至5.3um。
7. 循圓DBB驗證,在XY平面的測試中,未補償前的真圓度誤差為3.7微米(μm),經誤差補償後,顯著降低至2.6微米,改善幅度約30%。在YZ垂直平面的量測中,補償前的真圓度誤差為6.8um,補償後下降至4.9 um。XZ平面,補償前的真圓度誤差為11.5 um,為三個平面中最大,顯示原始在此方向的幾何偏差較為嚴重。然而經過補償後誤差顯著下降至6.4 um,改善幅度超過44%。其垂直度及直線度亦有提升。
當前研究成果顯示,透過21項幾何誤差補償技術,三軸工具機的空間精度與圓度精度均有顯著提升,為工具機高精度化奠定良好基礎。未來可朝以下幾個方向持續發展與精進:
(1) 誤差補償模型自動化與智慧化:結合感測技術與機器學習演算法,建構即時誤差辨識與補償系統,使工具機能於加工過程中自我調整誤差,提升自我診斷與自我修正能力。
(2) 高階誤差模型整合:除現有的21項自由度誤差外,進一步納入熱誤差、負載誤差及動態誤差等多因素,發展更完整的誤差模型,以因應複雜加工條件。
(3) 多軸與複合加工中心的應用擴展:將目前針對三軸工具機的誤差補償技術推廣至五軸或更多軸向的複合加工機種,以滿足高階零件製造對精度的更高需求。
(4) 標準化與模組化誤差補償流程:建立標準作業流程與模組化架構,使補償技術能廣泛應用於不同機型與製造環境,提升技術移植性與產業應用價值。
(5) 與數位雙生整合應用:將誤差補償模型整合進數位雙生(Digital Twin)平台,實現虛實同步監控與精度預測,強化智慧製造的可靠性與精度控制能力。
透過上述展望與持續精進,本技術有潛力成為推動高精度加工與智慧製造的關鍵技術之一,為未來產業升級與高階製造發展提供強大支撐。
參考資料
1. International Standard, "Geometric Accuracy Of Machines Operating Under No-Load or Quasi-Static Conditions", ISO230-1(2012).
2. International Standard, " Test code for machine tools Part 6: Determination of positioning accuracy on body and face diagonals (Diagonal displacement tests)", ISO230-6(2002).
3. https://www.renishaw.com/tw/
4. https://hexagon.com/
5. https://www.dmgmori.co.jp/zh_tw/
6. M.A.V. Chapman, "Limitations of laser diagonal measurements”, Precision Engineering 27 (2003), pages 401-406.
7. Renishaw, " Laser diagonal measurements for machine tool performance assessment”, Technical white paper : TE334





