使用掃描式測頭之五軸工具機雙旋轉軸幾何誤差同步量測系統

一、研究目的

現代製造技術的發展，高精度與高效率的加工需求增長，五軸工具機在航空航天、汽車製造等領域應用廣泛。然而高精度加工也帶來了複雜的誤差控制挑戰，直接影響成品品質及機台壽命，故五軸工具機的誤差量測成為重要研究課題。其中幾何誤差源於機床製造與組裝中的非理想幾何偏差，如軸向、角度、直線度等誤差，對加工品質影響顯著且會累積，故其量測與補償至關重要。

現商用儀器主要存在兩大問題：一是單次測量通常只針對少數幾何誤差項，忽略了其他誤差源的耦合效應及多軸同時運動時的誤差疊加。二是現有儀器多僅量測安裝誤差或單運動軸的誤差，忽視不同位置下運動誤差的影響。前人的研究已探討單軸運動旋轉軸誤差與雙軸運動下的安裝誤差，但鮮少兼顧兩者。故本文旨在開發針對五軸工具機的高精度幾何誤差量測技術，提出能同時解析雙旋轉軸共20項幾何誤差的系統，並考慮誤差耦合及動態影響。

二、研究方法

1.實驗設備、載具

本文使用的實驗載具為小型立式五軸加工機，圖1展示了其外觀。該機床具備全工作臺旋轉型設計，擁有五軸同步加工能力，其A軸與C軸的旋轉功能增加了工件定位的自由度，使工具幾乎能從任意角度接近工件，適合加工航空零件、汽車複雜元件及高精度模具等複雜外形部件。

圖1 立式五軸工具機

本文使用的量測設備為工具機上的測頭系統，該系統在高精度製造中扮演關鍵角色，確保加工精度、提升生產效率並優化製程。測頭系統透過精確測量工件與刀具位置，支持五軸加工機的高性能運作。

常見的觸發式測頭透過接觸工件表面觸發訊號，提供高精度的位置資訊，其可分為單點接觸式與掃描式測頭，單點接觸式測頭適用於點位量測，常用於簡單且精確的測量任務；掃描式測頭則能在工件表面連續移動，收集大量數據點，提供更詳細的表面輪廓資訊，適合複雜曲面和精細特徵的測量。

本文使用OSP60掃描式測頭系統（如圖2），與單點觸發測頭相比能快速沿著工件表面移動，收集大量數據點與方向資訊，特別適用大面積或多點測量的情況，有助於更精確地捕捉工件表面的輪廓及複雜幾何形狀，對於精度的質量控制尤為重要且縮短了測量時間，提高了細節分析與檢測能力。

圖2 OSP60掃瞄式測頭

2.量測系統、方法

本文開發之量測系統使用OSP60掃描式測頭進行量測，量測一良好的平面度之方塊與一高精度校正球。避免由球體半徑誤差帶來的量測不確定性及方塊表面平面度之影響。量測過程中，校正球磁吸於搖籃上，方塊則鎖固於轉臺，測頭安裝於主軸，具體安裝情況如圖3所示。測頭系統抓取校正球心及方塊固定點作為初始位置，隨後轉動雙旋轉軸並量測旋轉後的球心位置及方塊表面輪廓資訊。所有量測過程由NC code設計之自動程式完成，並將所得數據代入本文提出的數學模型中計算誤差。量測過程中需注意減少不確定性誤差來源，並確保所有設備經市售量測儀器補償及溫度控制，以得到最精確的結果。

圖3 實驗安裝照片

量測原理分為校正球與方塊兩部分。圖4顯示方塊安裝於C軸轉臺上，由於工具機零件在安裝時的不精確產生安裝誤差，C軸與A軸產生徑向偏移與偏擺，雙軸的誤差耦合影響方塊運動，使其移至Position1，並產生體積誤差dP (PIGE)。接著考慮運動誤差影響。

運動誤差來自於工具機零件製造時的瑕疵，導致零件之間的相對運動產生偏移與偏擺，使方塊產生另一體積誤差dP (PDGE)，並移動到Position2，Position2與ideal position即實際位置與理想位置之間的偏差，也就是總體積誤差dP。透過建立體積誤差與旋轉軸幾何誤差的關係，可以解析雙旋轉軸的安裝與運動誤差。系統透過擬合方塊尖點位置，量測方塊平面的法向量和一點位置，求出平面方程式，再聯立三個平面方程式計算尖點的機械座標值，避免測量誤差。接著考慮平面法向量的偏擺與旋轉軸幾何誤差之間的關係。

圖4顯示方塊尖點受幾何誤差影響產生體積誤差，使平面法向量出現方向上的體積偏擺dV，同理分為安裝誤差影響的dV(PIGE)和運動誤差影響的dV(PDGE)，其中僅偏擺誤差會影響法向量的方向。透過建立旋轉軸偏擺幾何誤差與法向量之間的關係，量測方塊上各平面法向量的偏差值即可求出體積誤差資訊以解析旋轉軸幾何誤差。

圖4 方塊受旋轉軸幾何誤差影響狀況

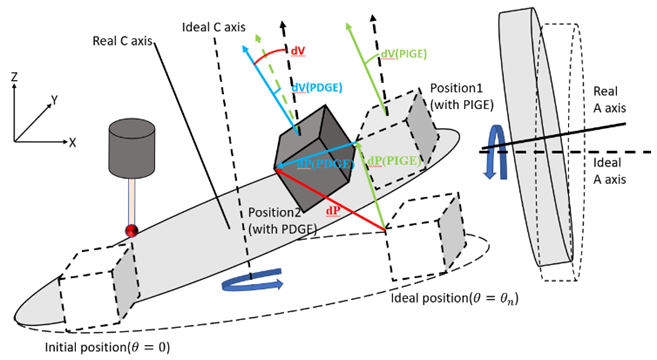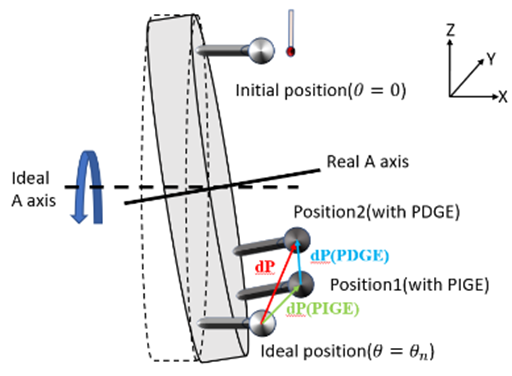
圖5顯示了校正球在幾何誤差影響下產生的偏差。本文的量測系統將校正球置於A軸搖籃機構上，因此當旋轉軸轉動時，球心位置只受A軸安裝誤差移動到Position1，再受運動誤差的影響移動到Position2，並產生體積誤差。這樣的設計可分離A軸幾何誤差的影響，同時解析轉台上方塊尖點的體積誤差，便於設計量測路徑。

圖5校正球受旋轉軸幾何誤差影響狀況

本文量測實驗具體流程如下，將掃描式測頭安裝於主軸，校正球置於A軸，方塊置於C軸。排除測頭誤差並在A、C軸角度為0的初始位置測量校正球與方塊的座標，執行自動量測程式進行各角度測量，記錄幾何資訊並計算誤差項。

測頭測量程序由NC code程式開發，通過圓路徑掃描、線路徑掃描及單點觸發進行自動測量，擬合出不同角度下校正球圓心座標與偏差(XYZ center error)、線路徑初始點法向量方向座標偏差(Start point error)與路徑角度偏差(Best fit angle)。

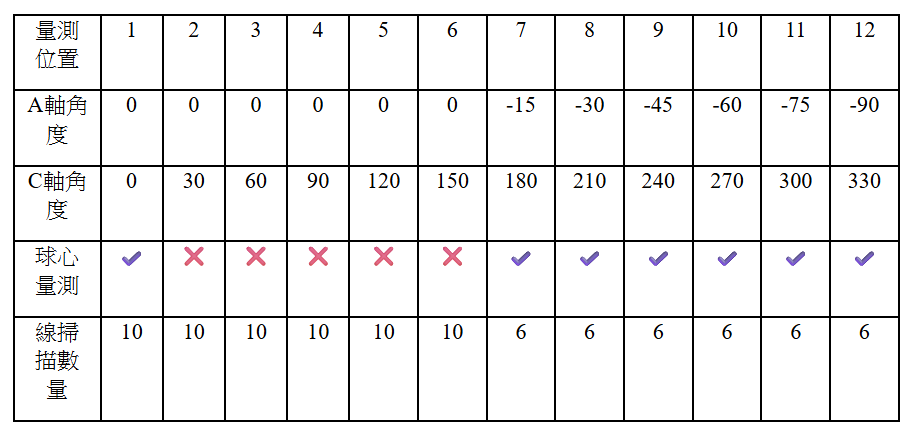
表1總結了12組旋轉軸位置與量測的關係。扣除初始位置，實驗共解析110個誤差項，包括A軸的安裝誤差(4項)與運動誤差(6自由度*6位置)及C軸的安裝誤差(4項)與運動誤差(6自由度*11位置)。A軸於初始位置和第7至12位置進行校正球量測XYZ center error，後六位置使用轉換後校正球座標進行測量。方塊五個平面各自生成兩條垂直路徑，通過路徑向量外積求得法向量，量測各平面的Start point error與 Best fit angle，透過上述資訊可以換算成體積誤差偏移與偏擺，用以解析幾何誤差，部分旋轉角度下由於姿態干涉問題略過某些平面測量。

表1 量測位置與旋轉軸角度對照

 

3.運動學

了解析幾何誤差，本文建立了測頭待測物的運動鏈關係，分別為：測頭P → Z軸 → Y軸 → X軸 → A軸 → C軸 → 方塊B，測頭P → Z軸 → Y軸 → X軸 → A軸 → 基準球S兩條運動鏈。由數學模型與齊次座標轉換矩陣以求得方塊與校正球相對測頭的關係。

 

在機械座標與各運動軸、待測物建立多個座標系，如工具機座標系、測頭座標系、校正球座標系等，並考慮各座標系間的距離參數，如各軸間距離和旋轉軸中心相對參考原點的距離，接著省略不影響結果之參數以優化後續運算，避免算式之冗長與無用之參數相乘項，圖6(a)與圖6(b)分別顯示了運動鏈簡化前與簡化後的結果。

圖6 初始未簡化運動鏈與簡化後運動鏈關係

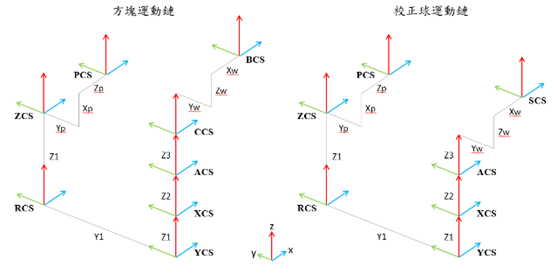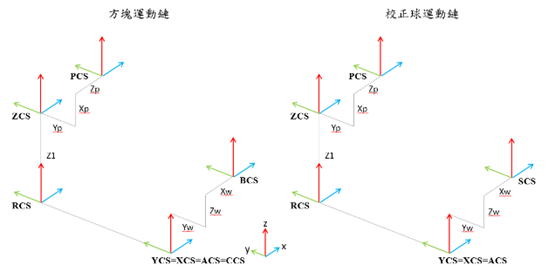(a)未簡化	(b)簡化後

 

        數學模型之推導方面，各座標系以齊次座標轉換矩陣表示其運動情形，接著根據相對幾何關係做矩陣的相乘，可得出各運動鏈對於機械原點之幾何關係，並分為理想與實際包含誤差之情形做運算，其結果包含了測頭尖點(probe center position)、校正球之球心座標(sphere center point)、方塊尖點之機械座標(block sharp point)、方塊平面之法向量(plane normal vector)等資訊。當測頭的探針尖點碰觸待測物時的位置是相同的條件可以視 測頭尖點與校正球球心重疊、或測頭尖點與方塊尖點重疊，並分為理想與實際情況下解出各運動軸之驅動值與， 理想與實際驅動相扣便可得出幾何資訊與旋轉軸幾何誤差之間的關係方程式，其中方程式變數包含量測角度和、方塊B和校正球S相對於旋轉軸座標系的座標值，並通過最小化殘差平方和來找到最佳的未知數解。在非線性情況下，可以使用迭代方法來近似求解，並將系統線性化來簡化求解過程。依照本實驗設計的量測路徑，計算不同旋轉軸角度位置下可獲得的方程式數量，一次量測可獲得180條方程式。將所有方程式的關係統整後得到A軸和C軸幾何誤差方程組並用以同時求解雙旋轉軸之幾何誤差。

 

三、實驗結果

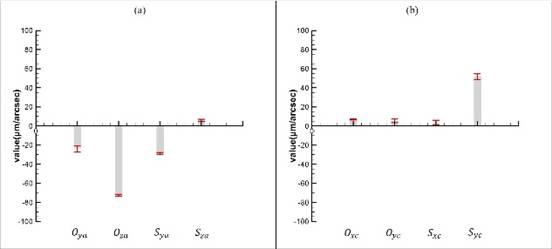
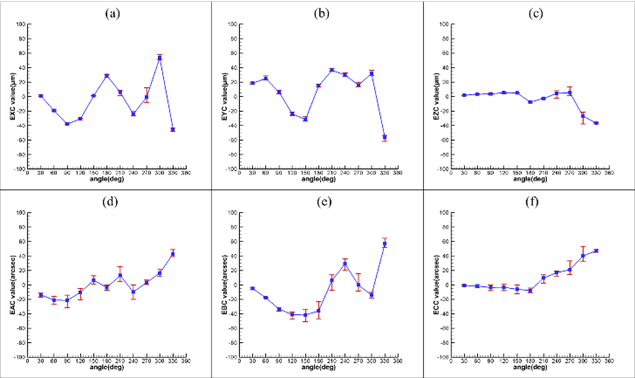
本文實際量測實驗取五組結果取平均並比對各組結果之間的重複性表現，量測結果如圖7至圖9所示，由圖7的量測結果分析，A軸的安裝誤差 分別為-23.1704µm、-72.8639µm、-29.0082arcsec、5.8683arcsec；C軸的安裝誤差 分別為7.0554µm、5.0641µm、3.6991arcsec、51.7812arcsec。A軸的偏移誤差和C軸的偏擺誤差較大，推測可能是其他零件的安裝誤差耦合造成，如線性軸的垂直度誤差。系統解析時假設線性軸無誤差，但實際上工具機存在線性軸誤差，影響旋轉軸的安裝誤差數值。

圖7 安裝誤差量測結果(a)A軸安裝誤差(b)C軸安裝誤差

圖8 A軸運動誤差量測結果(a)EXA (b)EYA (c)EZA (d)EAA (e)EBA (f)ECA

 

圖9 C軸運動誤差量測結果(a)EXC (b)EYC (c)EZC (d)EAC(e)EBC (f)ECC

 

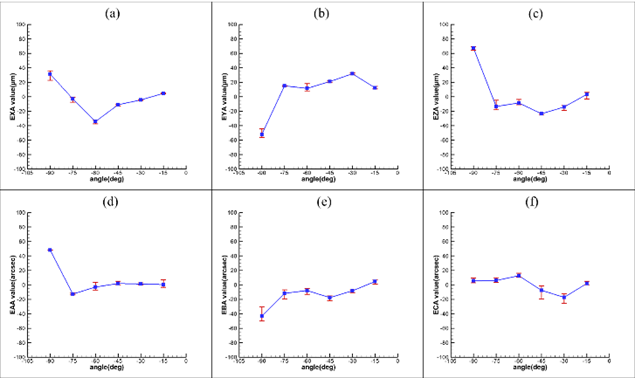
由於實驗機台無補償功能，且國內相關研究有限，本文採用數值比對法驗證量測誤差。現今機台製造廠商常用校正球定位法粗略估計旋轉軸偏差，具體作法是在初始位置定位球心座標，旋轉軸至180°再定位第二組座標，取兩者平均得出旋轉中心座標偏移值。若增加至每90°一組座標，通過擬合圓法可估算旋轉軸安裝誤差與偏擺。此法雖不能精確量測安裝誤差，但能大致推算旋轉中心與轉動情形。

本文針對A軸，因行程限制無法涵蓋完整圓路徑，改以30°區間抓取四個座標擬合最佳旋轉中心。隨後與前代學長發展的雙旋轉軸安裝誤差量測系統結果比對，顯示誤差分析結果基本相符。儘管各方法間有細微差距，可能由溫度或振動等不確定因素造成，但差異在可接受範圍內。前代學長發展的方法經過補償驗證具可靠性，擬合圓計算作為誤差評估方法也具一定準確性，因此本文驗證了誤差計算結果的正確性。

四、結論與未來

本文針對五軸工具機提出一套量測系統，可同時量測雙旋轉軸的20項幾何誤差。該系統採用掃描式測頭，具備動態量測功能，簡單校正後即可快速自動執行量測。此方法不僅能解析更多幾何誤差，還具備價格低、安裝操作便捷、測量時間短等優點。掃描式測頭技術是一項創新，能夠在移動中持續收集數據，相比傳統單點觸發式測頭，可更快地獲取工件表面的密集座標點，適合五軸加工機進行複雜工件的全面量測。此外，該系統靈活應對不同構型的五軸機台，只需修改數學模型與程式，即可解析各構型的幾何誤差，提供精確解決方案。

未來發展方向包括系統智能化、自動化及多功能測量。透過人工智能技術，測頭可實現自動校準與誤差補償，減少人工干預，提升測量精度與效率。亦可進一步擴展量測參數，如工件尺寸、形狀、表面粗糙度等，實現全面質量檢測。此外，亦可配合實時溫度補償技術可根據溫度傳感器數據自動修正測量結果，或利用熱膨脹係數模型進行調整。同時，主動振動控制技術將通過反向振動進行抑制，並結合振動補償算法修正測量結果，減少誤差影響。

參考文獻

[1]   S. Onishi, S. Ibaraki, T. Kato et al., “A Self-Calibration Scheme to Monitor Long-Term Changes in Linear and Rotary Axis Geometric Errors,” Measurement, vol. 196, p. 111183, 2022.

[2]   “Modeling Quasi-Static Errors in a Five-Axis Gantry Machine Tool”, https://www.scientific.net/AMM.152-154.781.pdf (accessed.

[3]  L. Andolfatto, S. Lavernhe, and J. R. R. Mayer, “Evaluation of Servo, Geometric and Dynamic Error Sources on Five-Axis High-Speed Machine Tool,” International Journal of Machine Tools and Manufacture, vol. 51, no. 10, pp. 787-796, 2011.

[4]   V. S. B. Kiridena and P. M. Ferreira, “Kinematic Modeling of Quasistatic Errors of Three-Axis Machining Centers,” International Journal of Machine Tools and Manufacture, vol. 34, no. 1, pp. 85-100, 1994.

[5]   S. Ibaraki, M. Sawada, A. Matsubara et al., “Machining Tests to Identify Kinematic Errors on Five-Axis Machine Tools,” Precision Engineering, vol. 34, no. 3, pp. 387-398, 2010.

[6]   S. Ibaraki, T. Iritani, and T. Matsushita, “Calibration of Location Errors of Rotary Axes on Five-Axis Machine Tools by on-the-Machine Measurement Using a Touch-Trigger Probe,” International Journal of Machine Tools and Manufacture, vol. 58, pp. 44-53, 2012.

[7]   C. Hong, S. Ibaraki, and C. Oyama, “Graphical Presentation of Error Motions of Rotary Axes on a Five-Axis Machine Tool by Static R-Test with Separating the Influence of Squareness Errors of Linear Axes,” International Journal of Machine Tools and Manufacture, vol. 59, pp. 24-33, 2012.

[8]   S. Ibaraki and K. Tsuboi, ““Open-Loop” Tracking Interferometer Measurement Using Rotary Axes of a Five-Axis Machine Tool,” IEEE/ASME Transactions on Mechatronics, vol. 22, no. 5, pp. 2342-2350, 2017.

[9]   S. Ibaraki, Y. Kimura, Y. Nagai et al., “Formulation of Influence of Machine Geometric Errors on Five-Axis on-Machine Scanning Measurement by Using a Laser Displacement Sensor,” Journal of Manufacturing Science and Engineering, vol. 137, no. 2, 2015.

[10] H. Wang and X. Jiang, “Geometric Error Identification of Five-Axis Machine Tools Using Dual Quaternion,” International Journal of Mechanical Sciences, vol. 229, p. 107522, 2022.